The Quadratic Formula is a well known formula for finding the roots of a parabola described by $f(x) = ax^2 + bx + c = 0$ , with $a, b$ and $c$ some real values. By plugging the values of $a, b$ and $c$ into the Quadratic Equation $x = \frac{-b \pm \sqrt{b^2 -4ac}}{2a}$ , one obtains the values $x$ for which the parabola intersects with the x-axis. This is the method for computing the roots of such a function, but I’m very bad in remembering the Quadratic Equation exactly. When I was a High School student I sometimes mixed up the signs and/or values, resulting in a lower math grade. Therefore I decided to figure out why the Quadratic Formula is as it is and how you can derive it in case you have no internet or math book with you. The derivation is quite straight-forward, but the important part is how to reason about the problem and working towards a solution.

Derivation

The following figure shows such a parabola (or 2nd degree polynomial) with $a=1, b=-1, c=-1$ . It is important to note that a parabola is symmetric around some vertical axis at $x_c$ . This observation is essential for understanding the derivation. Furthermore, due to this symmetry, the distances between each root $x_{0,1}$ and the center $x_c$ are identical.

Rendered by QuickLaTeX.com

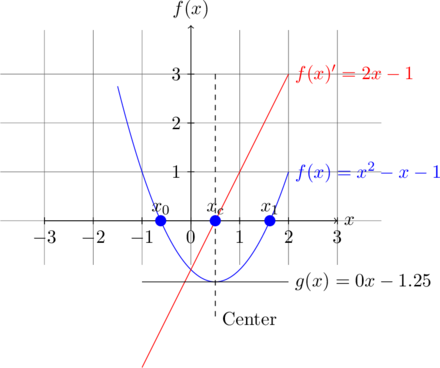
In order to find the roots of the parabola, we need to find center $x_c$ first. At this center $x_c$ , the minimum (or maximum) of the parabola is located. Furthermore, we can clearly see that at this minimum the slope of the tangential line is zero (see $g(x)$ ). But how can we find an $x$ for which the tangential is zero?

Using the derivative of a function, one can obtain the slope of this tangential line for some value of $x$ . Sounds complicated, but look closer to the plot above. Function $g(x)$ is our tangential line of the parabola at $x_c$ and its slope is zero (due to $0x$ ). Function $f(x)=x^2-x-1$ is our parabola and $f(x)'=2x-1$ its derivative which is zero exactly at center $x_c$ ! So, in order to compute $x_c$ , we need to solve $f(x)'=2x-1=0$ for $x$ . Using some basic algebra one can find that $x=x_c=1/2$ fulfils this, which is correct according to the plot.

To be more general, function $f(x)=ax^2+bx+c$ has a derivative $f(x)'=2ax+b$ . To find $x_c$ we solve $f(x)'=2ax+b=0$ for $x$ , which is $x=\frac{-b}{2a}$ .

Now we have found the center of a parabola, we continue with deriving a formula for computing $x_0$ and $x_1$ . Since the distances between the center and the roots are identical, we can also say $x_{0,1} = x_c \pm d$ , with $d$ the unknown distance between a root and the center. Furthermore, we known that for a root $x_{0,1}$ function $f(x_{0,1}) = ax_{0,1}^2 + bx_{0,1}+c = 0$ . To find the roots, we substitute $x_{0,1}$ with $x_c \pm d$ and solve the equation for our unknown distance $d$ . Here the fun starts and you might recognize some parts of the Quadratic Equation.

First we substitute $x$ in $f(x)$ with $\frac{-b}{2a} + d$ (we use a plus sign here, since it doesn’t matter for the derivation) and solve for $d$ . (For clarity, I show all steps in the derivation in order to make things clear.)

$a(\frac{-b}{2a} + d)^2 + b(\frac{-b}{2a} + d) + c = 0$

$a(\frac{b^2}{4a^2}+d^2-\frac{2bd}{2a}) + b(\frac{-b}{2a} + d) + c = 0$

$\frac{ab^2}{4a^2} + ad^2 -\frac{2abd}{2a}-\frac{b^2}{2a} + bd + c = 0$

$\frac{b^2}{4a} + ad^2 -bd - \frac{b^2}{2a} + bd + c = 0$

$\frac{b^2}{4a} + ad^2 - \frac{2b^2}{4a} + c = 0$

$-\frac{b^2}{4a} + ad^2 + c = 0$

$ad^2 = \frac{b^2}{4a} - c$

$d^2 = \frac{\frac{b^2}{4a} - c}{a}$

$d^2 = \frac{b^2}{4a^2} - \frac{c}{a}$

$d^2 = \frac{b^2}{4a^2} - \frac{4ac}{4a^2}$

$d^2 = \frac{b^2 - 4ac}{4a^2}$

$d = \pm\sqrt{\frac{b^2 - 4ac}{4a^2}}$

$d = \pm\frac{\sqrt{b^2 - 4ac}}{2a}$

Now we have derived a function for computing the distance between a root and the center. In order to obtain $x_0$ and $x_1$ , we plug the formula for $d$ into the formula $x_{0,1} = \frac{-b}{2a}\pm d$ , which gives:

$x_{0,1} = \frac{-b}{2a} \pm \frac{\sqrt{b^2 - 4ac}}{2a} = \frac{-b \pm \sqrt{b^2-4ac}}{2a}$ ,

which is exactly the Quadratic Formula $\blacksquare$ .